Fitting a psychometric function at the group level#

Author: Nicolas Legrand nicolas.legrand@cas.au.dk

import pytensor.tensor as pt
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from scipy.stats import norm
import pymc as pm

sns.set_context('talk')

In this example, we are going to fit a cummulative normal function to decision responses made during the Heart Rate Discrimination task. We will use the data from the HRD method paper [Legrand et al., 2022] and analyse the responses from all participants and infer group-level hyperpriors.

# Load data frame
psychophysics_df = pd.read_csv('https://github.com/embodied-computation-group/CardioceptionPaper/raw/main/data/Del2_merged.txt')

First, let’s filter this data frame so we only keep the interoceptive condition (Extero label).

this_df = psychophysics_df[psychophysics_df.Modality == 'Extero']
this_df.head()
TrialType Condition Modality StairCond Decision DecisionRT Confidence ConfidenceRT Alpha listenBPM ... EstimatedThreshold EstimatedSlope StartListening StartDecision ResponseMade RatingStart RatingEnds endTrigger HeartRateOutlier Subject
1 psi Less Extero psi Less 2.216429 59.0 1.632995 -0.5 78.0 ... 22.805550 12.549457 1.603353e+09 1.603354e+09 1.603354e+09 1.603354e+09 1.603354e+09 1.603354e+09 False sub_0019
3 psiCatchTrial Less Extero psiCatchTrial Less 1.449154 100.0 0.511938 -30.0 82.0 ... NaN NaN 1.603354e+09 1.603354e+09 1.603354e+09 1.603354e+09 1.603354e+09 1.603354e+09 False sub_0019
6 psi More Extero psi More 1.182666 95.0 0.606786 22.5 69.0 ... 10.001882 12.884902 1.603354e+09 1.603354e+09 1.603354e+09 1.603354e+09 1.603354e+09 1.603354e+09 False sub_0019
10 psi More Extero psi More 1.848141 24.0 1.448969 10.5 62.0 ... 0.998384 13.044744 1.603354e+09 1.603354e+09 1.603354e+09 1.603354e+09 1.603354e+09 1.603354e+09 False sub_0019
11 psiCatchTrial More Extero psiCatchTrial More 1.349469 75.0 0.561820 10.0 72.0 ... NaN NaN 1.603354e+09 1.603354e+09 1.603354e+09 1.603354e+09 1.603354e+09 1.603354e+09 False sub_0019

5 rows × 25 columns

This data frame contain a large number of columns, but here we will be interested in the Alpha column (the intensity value) and the Decision column (the response made by the participant).

this_df = this_df[['Alpha', 'Decision', 'Subject']]
this_df.head()
Alpha Decision Subject
1 -0.5 Less sub_0019
3 -30.0 Less sub_0019
6 22.5 More sub_0019
10 10.5 More sub_0019
11 10.0 More sub_0019

These two columns are enought for us to extract the 3 vectors of interest to fit a psychometric function:

  • The intensity vector, listing all the tested intensities values

  • The total number of trials for each tested intensity value

  • The number of “correct” response (here, when the decision == ‘More’).

Let’s take a look at the data. This function will plot the proportion of “Faster” responses depending on the intensity value of the trial stimuli (expressed in BPM). Here, the size of the circle represent the number of trials that were presented for each intensity values.

Model#

The model is defined as follows:

\[ r_{i} \sim \mathcal{Binomial}(\theta_{i},n_{i})\]
\[ \Phi_{i, j}(x_{i, j}, \alpha, \beta) = \frac{1}{2} + \frac{1}{2} * erf(\frac{x_{i, j} - \alpha}{\beta * \sqrt{2}})\]
\[ \alpha_{i} \sim \mathcal{Normal}(\mu_{\alpha}, \sigma_{\alpha})\]
\[ \beta_{i} \sim \mathcal{Normal}(\mu_{\beta}, \sigma_{\beta})\]
\[ \mu_{\alpha} \sim \mathcal{Uniform}(-50, 50)\]
\[ \sigma_{\alpha} \sim |\mathcal{Normal}(0, 100)|\]
\[ \mu_{\beta} \sim \mathcal{Uniform}(0, 100)\]
\[ \sigma_{\beta} \sim |\mathcal{Normal}(0, 100)|\]

Where \(erf\) is the error functions, and \(\Phi\) is the cumulative normal function with threshold \(\alpha\) and slope \(\beta\).

We create our own cumulative normal distribution function here using pytensor.

def cumulative_normal(x, alpha, beta):
    # Cumulative distribution function for the standard normal distribution
    return 0.5 + 0.5 * pt.erf((x - alpha) / (beta * pt.sqrt(2)))

We preprocess the data to extract the intensity \(x\), the number or trials \(n\) and number of hit responses \(r\). We also create a vector sub_total containing the participants index (from 0 to \(n_{participants}\)).

nsubj = this_df.Subject.nunique()
x_total, n_total, r_total, sub_total = [], [], [], []

for i, sub in enumerate(this_df.Subject.unique()):

    sub_df = this_df[this_df.Subject==sub]

    x, n, r = np.zeros(163), np.zeros(163), np.zeros(163)

    for ii, intensity in enumerate(np.arange(-40.5, 41, 0.5)):
        x[ii] = intensity
        n[ii] = sum(sub_df.Alpha == intensity)
        r[ii] = sum((sub_df.Alpha == intensity) & (sub_df.Decision == "More"))

    # remove no responses trials
    validmask = n != 0
    xij, nij, rij = x[validmask], n[validmask], r[validmask]
    sub_vec = [i] * len(xij)

    x_total.extend(xij)
    n_total.extend(nij)
    r_total.extend(rij)
    sub_total.extend(sub_vec)

Create the model.

with pm.Model() as group_psychophysics:

    mu_alpha = pm.Uniform("mu_alpha", lower=-50, upper=50)
    sigma_alpha = pm.HalfNormal("sigma_alpha", sigma=100)

    mu_beta = pm.Uniform("mu_beta", lower=0, upper=100)
    sigma_beta = pm.HalfNormal("sigma_beta", sigma=100)

    alpha = pm.Normal("alpha", mu=mu_alpha, sigma=sigma_alpha, shape=nsubj)
    beta = pm.Normal("beta", mu=mu_beta, sigma=sigma_beta, shape=nsubj)

    thetaij = pm.Deterministic(
        "thetaij", cumulative_normal(x_total, alpha[sub_total], beta[sub_total])
    )

    rij_ = pm.Binomial("rij", p=thetaij, n=n_total, observed=r_total)

pm.model_to_graphviz(group_psychophysics)
../../_images/763ef7ce0789d00abcdcba7921c783fec0b3a2882112a45bd4b85441a04fa6ea.svg

Sampling.

with group_psychophysics:
    idata = pm.sample(chains=4, cores=4)

Auto-assigning NUTS sampler...

Initializing NUTS using jitter+adapt_diag...

Multiprocess sampling (4 chains in 4 jobs)

NUTS: [mu_alpha, sigma_alpha, mu_beta, sigma_beta, alpha, beta]
100.00% [8000/8000 03:06<00:00 Sampling 4 chains, 0 divergences] 
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 187 seconds.

az.plot_trace(idata, var_names=["mu_alpha", "alpha"]);
../../_images/1bafebccb2d792c7e3c43676a415c8f4eef8bbceb6e85a6e21c967069f764c3d.png 
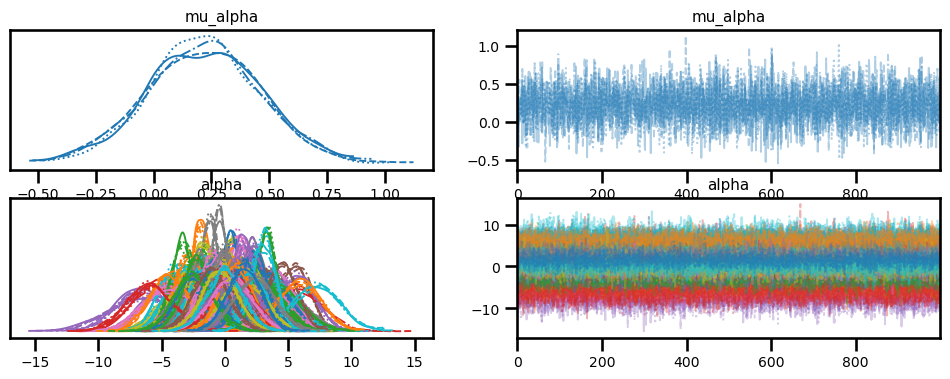
stats = az.summary(idata, var_names=["mu_alpha", "mu_beta"])
stats
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
mu_alpha 0.216 0.235 -0.248 0.641 0.004 0.003 4254.0 3189.0 1.0
mu_beta 7.922 0.232 7.479 8.342 0.004 0.003 2755.0 2885.0 1.0 


az.plot_posterior(idata, var_names=["mu_alpha"])

<Axes: title={'center': 'mu_alpha'}>
../../_images/4e6579ce798f4787f35d076609231d586882700855e0fffcd18f4663aad4d2bc.png

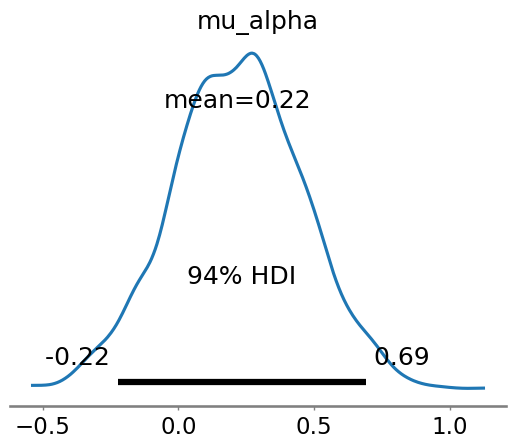
Plotting#

Extrace the individual parameters estimates.

alpha_samples = az.summary(idata, var_names=["alpha"])["mean"].values
beta_samples = az.summary(idata, var_names=["beta"])["mean"].values

fig, axs = plt.subplots(figsize=(8, 6))

# Draw some sample from the traces
for a, b in zip(alpha_samples, beta_samples):
    axs.plot(
        np.linspace(-40, 40, 500), 
        (norm.cdf(np.linspace(-40, 40, 500), loc=a, scale=b)),
        color='gray', alpha=.05, linewidth=2
    )

# Plot psychometric function with average parameters
slope = az.summary(idata, var_names=["mu_beta"])['mean']['mu_beta']
threshold = az.summary(idata, var_names=["mu_alpha"])['mean']['mu_alpha']
axs.plot(np.linspace(-40, 40, 500), 
        (norm.cdf(np.linspace(-40, 40, 500), loc=threshold, scale=slope)),
         color='#4c72b0', linewidth=4)

axs.plot([threshold, threshold], [0, .5], '--', color='#4c72b0', linewidth=2)
axs.plot(threshold, .5, 'o', color='w', markeredgecolor='#4c72b0', 
         markersize=15, markeredgewidth=3)

plt.ylabel('P$_{(Response = More|Intensity)}$')
plt.xlabel('Intensity ($\Delta$ BPM)')
plt.title('Group level estimate of the psychometric function')
plt.tight_layout()
sns.despine()
../../_images/70591fd4398c14197fea5ea6a60b547b4c50542123b0c491a93ccc30d770312a.png

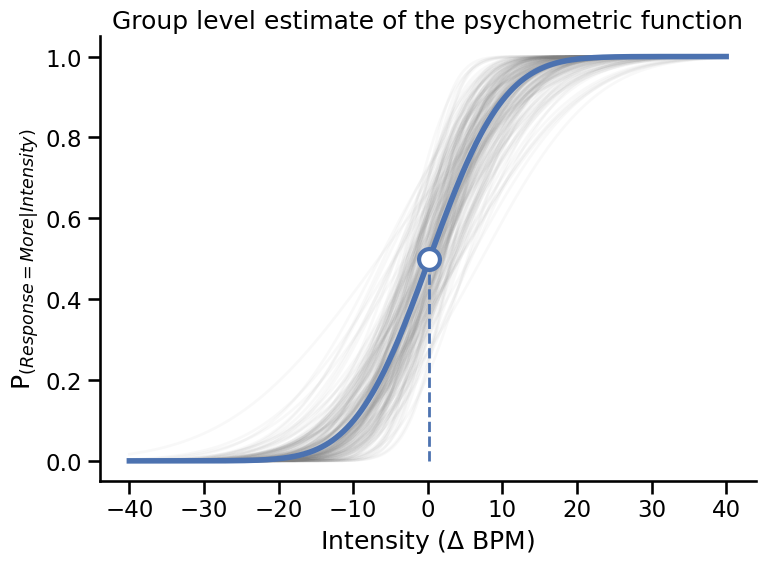
System configuration#

%load_ext watermark
%watermark -n -u -v -iv -w -p pymc,arviz,pytensor

Last updated: Wed Nov 08 2023

Python implementation: CPython
Python version       : 3.9.18
IPython version      : 8.17.2

pymc    : 5.9.1
arviz   : 0.16.1
pytensor: 2.17.3

pymc      : 5.9.1
seaborn   : 0.13.0
matplotlib: 3.8.1
pytensor  : 2.17.3
numpy     : 1.22.0
arviz     : 0.16.1
pandas    : 2.0.3

Watermark: 2.4.3